Quickstart

Take a small-scale nonlinear New Keynesian model with ZLB as a starting point, which is provided as an example (find the yaml file here). Here is how to simulate it and plot nonlinear impulse responses. Start with some misc imports and load the package:

import matplotlib.pyplot as plt
import econpizza as ep

# only necessary if you run this in a jupyter notebook:
%matplotlib inline

Next, load the model and solve for the steady state.

# the path to the example YAML
example_nk = ep.examples.nk

# load the NK model
mod = ep.load(example_nk)
_ = mod.solve_stst()

WARNING:jax._src.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

(load:) Parsing done.
    Iteration   1 | max. error 7.89e-01 | lapsed 0.4894
    Iteration   2 | max. error 5.07e-01 | lapsed 0.5595
(solve_stst:) Steady state found (0.69372s). The solution converged.

Finally, set a 4% discount factor shock and simulate it:

# shock the discount factor by 4%
shk = ('e_beta', .04)

# find the nonlinear trajectory
x, flag = mod.find_path(shock=shk)

    Iteration   1 | max error 1.71e-01 | lapsed 0.7477s
    Iteration   2 | max error 3.89e-01 | lapsed 0.7514s
    Iteration   3 | max error 2.35e-01 | lapsed 0.7544s
    Iteration   4 | max error 2.50e-01 | lapsed 0.7573s
    Iteration   5 | max error 6.81e-02 | lapsed 0.7601s
    Iteration   6 | max error 2.14e-02 | lapsed 0.7629s
    Iteration   7 | max error 5.58e-06 | lapsed 0.7656s
    Iteration   8 | max error 3.97e-12 | lapsed 0.7683s
(find_path:) Stacking done (0.886s).

The rest is plotting…

# plotting
fig, axs = plt.subplots(2,2)
for i,v in enumerate(('y', 'pi', 'r', 'beta')):

    axs.flatten()[i].plot(x[:35,mod['variables'].index(v)])
    axs.flatten()[i].set_xlabel(v)

fig.tight_layout()

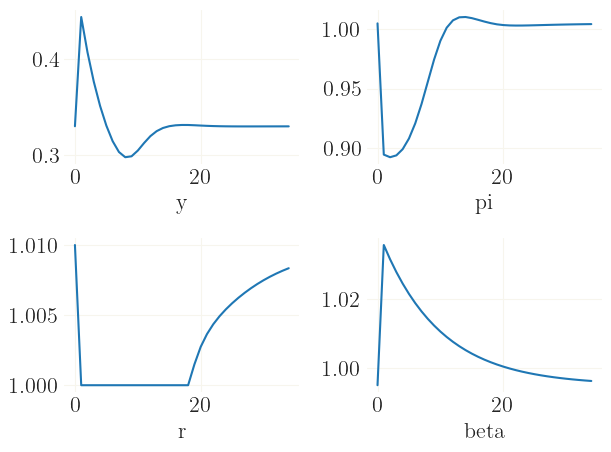
The impulse responses are the usual dynamics of a nonlinear DSGE model with the zero-lower bound on nominal interest rates.

Alternatively to specifying a shock, you can instead provide the initial conditions:

# use the jax implementation of numpy
import jax.numpy as jnp

# get the steady state as initial condion
x0 = mod['stst'].copy()
# and emulate again a 4% shock
x0['beta'] *= 1.04

# solving...
x, flag = mod.find_path(init_state=x0.values())

# plotting...
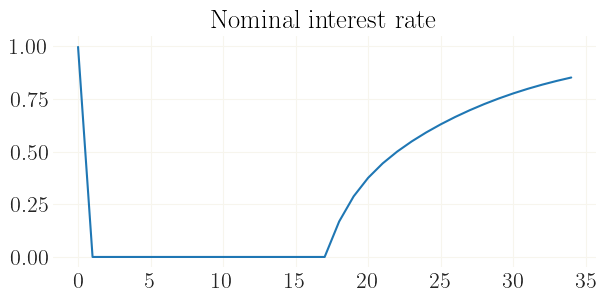
plt.figure(figsize=(7,3))
plt.plot(100*jnp.log(x[:35,mod['variables'].index('r')]))
plt.title('Nominal interest rate')

    Iteration   1 | max error 1.51e-01 | lapsed 0.0034s
    Iteration   2 | max error 2.92e-01 | lapsed 0.0066s
    Iteration   3 | max error 1.57e-01 | lapsed 0.0095s
    Iteration   4 | max error 3.66e-02 | lapsed 0.0124s
    Iteration   5 | max error 3.93e-03 | lapsed 0.0151s
    Iteration   6 | max error 3.90e-05 | lapsed 0.0177s
    Iteration   7 | max error 5.68e-10 | lapsed 0.0203s
(find_path:) Stacking done (0.092s).

Text(0.5, 1.0, 'Nominal interest rate')